技术类的可以考虑org-present
也可以考虑reveal.js,全平台通吃
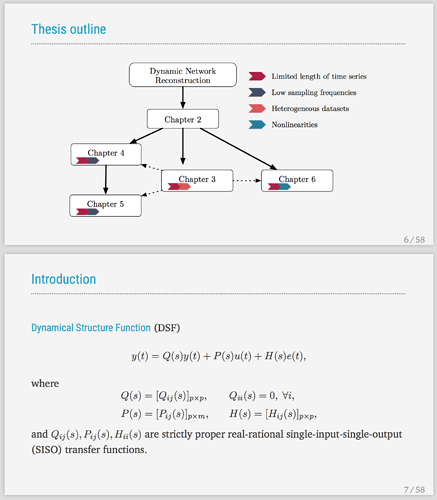
如果你学术报告多,可以用LaTeX的beamer做,也可以很漂亮,关键是排版省心(只要你不是花里胡哨党),特别公式多的时候,给你个截图看看。它生成PDF,只要你有PDF阅读器,全屏播放就成,也可以用激光笔翻页。工科、数学物理类会议PPT绝大多数都是latex做的,当然生物、人文用的不多。
当然如果你图文想搞的很艺术的自由排列,这时候我是用Keynote的(Mac),Linux下Libre Office或WPS也还不错,足够用了。
这个是什么主题
这里来一堆Beamer Themes Gallery - Templates, Examples and Articles written in LaTeX - Overleaf, Online LaTeX Editor
我自己做的,主题配色从一个Emacs主题里提出来的
修改是基于这个Solarized的模板,你把它换成你喜欢的主题配色就好了
哈,给你来个更plain的,我给学生准备ppt都用这种(自己仿制了一个 ),确保他们没任何可能看着五彩斑斓无思乱想 
其实这种黑白的最好看!
哈哈,点开学习了一下对函数性质的判断。
(☞゚ヮ゚)☞ 数学系老师?
在第 3-2 页,遇到一个问题:
比如速度矢量和压力标量满足下面两个方程:
都是常数,
是时间。
如何才能判定速度矢量 (v) 的凹凸性质( concave or convex ) 呢?
(请忽略我,如果我在错误地方问了错误的问题 (¯\__(ツ)_/¯))
不不不,我只是个TA而已
这个我也没思路怎么判断,我不是很懂偏微
哈哈,没事没事,以后遇到了到 stack*over* 上去问。
这个 ppt 很好啊,保证他们不开小差 : )
这才是最好的
非常喜欢这种性冷淡风格
我觉的从微分方程判断其解函数的凹凸性还是很难的。
比如说,我了解的Robust Control,讨论LTI system,是线性时不变的常微分方程,其条件保证解的凹/凸性依然是非常复杂的。至于偏微,我想直接跪 
Reference:
- Dullerud G.E., Paganini F.-A Course in Robust Control Theory - A Convex Approach-Springer (2005)
国企混的离不开office,领导个个是脑残,推荐
那天我也不知道自己的脑回路怎么搞的,不知道啥时候看到了有好事的人悬赏了 100 万美金来解决 我在 20 楼 提到的那两个方程组。
从你的 PPT 上,我突然想到,如果能对一个方程的凹凸性质有了比较直观的了解,或许其有无解的可能就有可能被解决。
我说么,怎么这么眼熟像无旋流体类的方程。
你的确想多了,这个方程,和黎曼猜想一起,这两个问题祸祸了多少天才数学家了