目录
这里 是原文链接
毕竟是 60 年前的文章,当时深奥的概念在现代可能也就小学生水平。我总结了这篇论文里比较吸引人的几点:
-
这篇论文 并不是 定义了 LISP 的文章。这篇论文发表之前,LISP 就已经存在于现实中了。不过应该可以把这篇论文中的 LISP 视作最初的 LISP。
-
这篇论文中,用于表达数据的是 S-表达式,而用于表达计算的是 M-表达式(还有一种没什么存在感的 L-表达式)。虽说它们之间有一个非常自然的对应关系,但是它们终究还是不同,似乎也导致了刚开始人们并没有发明宏。
-
“条件判断” 在这篇论文中首创。此前的程序员通过条件跳转指令(或者类似的东西,像是 FORTRAN 中那样)来实现条件判断。McCarthy 可能已经在 FORTRAN 里实现了条件判断的 函数 ,但是无法满足 “只做必要的计算”的需求,所以把条件判断规定为了 LISP 的原语。
-
“垃圾回收” 也是这篇论文中首次提出的(包括这个名字)。这种方式和列表相性不错,因为能利用上所有碎片化的内存。
-
然而更为知名的列表却并不是 LISP 首创的,§7 参考文献 2 中首次提出了列表。但是该论文中并没有提出垃圾回收,其中的内存管理机制为:维护一个“available-space” 列表,需要内存时从中取出一个地址,删去列表元素时将其地址放入 “available-space” 列表中。§7 参考文献 2 似乎没有考虑多个列表共享尾部结构的情况。并且这个操作无法释放元素(element,§7 参考文献 2 中意为 “原子”)所占据的内存。
来自他人的读书笔记:
此外,也推荐阅读 McCarthy 后来编写的 History of Lisp。
1. 简介
作者:John McCarthy,麻省理工学院,马萨诸塞州剑桥市。
麻省理工学院的人工智能小组为 IBM 704 计算机开发了一种名为 LISP(表示列表处理器,LISt Processor)的程序系统。该系统旨在促进对拟议的称为“Advice Taker” 的系统的实验,通过该系统,可以指示机器处理陈述句和祈使句,并在执行命令时表现出 “常识”(common sense)。关于 Advice Taker 的最初方案(§7 参考文献 1)在 1958 年 11 月提出。主要要求是建立一个程序系统,用于操作表示形式化陈述句和祈使句的表达式,以便 Advice Taker 系统可以进行推论。
LISP 系统在发展过程中经历了几个简化阶段,最终方案基于表示符号表达式的缺漏递归函数(partial recursive function)。这种表示独立于 IBM 704 计算机(当然也独立于其他电子计算机),所以从所谓 “S-表达式” 和 “S-函数”开始阐述系统应该挺合理。
在本文中,我们首先描述了递归定义函数的形式。我们认为这种形式无论作为编程语言还是计算理论的开发工具都有优势。接下来,我们描述 S-表达式和 S-函数,举一些例子,然后描述泛应用3 S-函数 apply。于理论,它是通用图灵机;于实际,它是 LISP 解释器。接下来,我们通过类似于 Newell、Shaw 和 Simon(§7 参考文献 2)使用的列表结构,在 IBM 704 内存表示 S-表达式,然后用程序表示 S-函数。之后我们提到 IBM 704 上 LISP 程序系统的主要功能。接下来是另一种用符号表达式描述计算的方法。最后我们用递归函数解释了流程图。
我们希望在另一篇论文中描述 LISP 用于的一些符号计算,并在其他地方将我们的递归函数形式应用于数理逻辑和机械定理证明问题。
2. 函数及其定义
我们将需要一些关于一般函数的数学思想和符号。大多数想法都是众所周知的,但条件表达式的概念应该是新的4,我们可以用它以一种新的便利方式定义递归函数。
2.1. 缺漏函数(partial function)
缺漏函数指,只对定义域的一部分定义了返回值的函数。缺漏函数对计算来说是必要的,因为(比方说)计算可能陷入无限递归,这时函数的返回值是未定义的。我们的一些基本函数也会被定义为缺漏函数。
2.2. 命题表达式与谓词(propositional expression, predicate)
命题表达式指返回值只有可能是 T (表示真)或者 F (表示假)的表达式。我们可以在命题表达式中使用常见的数学连词,也就是与或非(∧, ∨, ¬)。典型的命题表达式是:
x < y
(x < y) ∧ (b = c)
x 是质数
谓词指返回值要么是 T ,要么是 F 的函数。
2.3. 条件表达式(Conditional Expression)
在数学中,真值对其他类型的值的依赖关系用谓词表示,真值对其他真值的依赖关系用逻辑连词表示。然而,表达其他类型的值对真值的依赖关系的数学符号不够多,所以这种关系的表示通常需要用到中文短语。比方说绝对值函数 |x| 就通常用中文来定义。条件表达式是表达一般表达式和命题表达式之间关系的一种工具。条件表达式形如:
(p₁ → e₁, p₂ → e₂, ⋯, pₙ → eₙ)
其中 p₁, p₂, ⋯, pₙ 为命题表达式, e₁, e₂, ⋯, eₙ 为任意表达式。可以读作“如果 p₁ ,那么 e₁ ,否则如果 p₂ ,那么 e₂ ,……,否则如果 pₙ ,那么 eₙ ” 或者 “p₁ 则 e₁ , p₂ 则 e₂ ,……, pₙ 则 eₙ ”5。
接下来我们给出条件表达式的求值方式,以及它的值是否有定义的判断方式。从左到右检测 p 的值,如果遇到了值为 T 的 pi ,并且这时还没有遇到未定义的 p ,那么整个条件表达式的值就是对应的 ei (如果有定义);如果在检测到值为 T 的 p 之前就检测到了未定义的 p ,或者所有 p 的值都是 F ,或者 ei 的值未定义,那么该条件表达式的值是未定义的。比方说:
- (1 < 2 → 4, 1 > 2 → 3) = 4
- (2 < 1 → 4, 2 > 1 → 3, 2 > 1 → 2) = 3
- (2 < 1 → 4, T → 3) = 3
- (2 < 1 → 0/0, T → 3) = 3
- (2 < 1 → 3, T → 0/0) 的值未定义
- (2 < 1 → 3, 4 < 1 → 4) 的值未定义
顺便也给一些简单的实际应用。
- |x| = (x < 0 → -x, T → x)
- δi, j = (i = j → 1, T → 0)
- sgn(x) = (x < 0 → -1, x = 0 → 0, T → 1)
2.4. 递归的函数定义
通过条件表达式,我们可以在函数定义体中使用它自己,同时避免无限循环。比方说,
n! = (n = 0 → 1, T → n⋅(n-1)!)
那么我们求值 0! 的结果是 1;因为函数的定义方式,没有意义的 0⋅(0-1)! 求值的结果并不会出现。再比如说 2! 的求值过程是:
2! = (2 = 0 → 1, T → 2 ⋅ (2-1)!)
= 2⋅1!
= 2⋅(1 = 0 → 1, t → 1⋅(1-1)!)
= 2⋅1⋅0!
= 2⋅1⋅(0 = 0 → 1, t → 0⋅(0-1)!)
= 2⋅1⋅1
= 2
我们再给出其它两个递归函数的定义。第一个是最大公因数(Greatest Common Divisor),我们根据欧几里得辗转相除法可以将它定义为:
gcd(m, n) = (m > n → gcd(n, m), m 整除 n → m, T → gcd(n mod m, m))
其中 n mod m 表示用 m 除 n 后得到的余数。
牛顿迭代法是一种求指定数字平方根估计值的算法。设指定的数字为 a ,初始估计值为 x ,可接受的估计值 y 需要满足 |y2 − a| < ε ,可以写成:
sqrt(a, x, ε) = (|x2 - a| < ε → x, T → sqrt(a, (x + a/x)/2, ε))
也有多个函数组合而成的递归,我们有需要的时候会用到这种递归。
不能保证递归函数一定会终止,比方说上面的 n! 在 n < 0 时就是如此。如果递归不会终止,那么将返回值视作未定义。
逻辑连词也可以用条件表达式定义:
p ∧ q = (p → q, T → F)
p ∨ q = (p → T, T → q)
¬p = (p → F, T → T)
p ⊃ q = (p → q, T → T)
如果我们考虑未定义的值,那么 ∧ 和 ∨ 并不是可交换运算。假如 p 是 F , q 是未定义,那么根据上面的定义 p ∧ q 是 F ,但是 q ∧ p 却是未定义。对于我们的应用领域来说这种行为其实是应该的,因为 p ∧ q 求值时首先会求值 p ,如果它为 F 那么 q 不会被求值。如果 p 的计算没有终止,那么我们永远没有办法计算 q 。我们今后以此种意味使用逻辑连词。
2.5. 函数、形式(function, form)
函数通常用于数学中,用于指代 y2 + x 这样的形式。但是我们接下来的计算会涉及 “求值为函数的表达式”,所以我们需要区分函数和形式,并且需要一种记法来表达出它们的差异。我们选用了丘奇(Church,λ 演算发明人)的方式。
令 f 为一个表达式,其表示一个函数,有刚好两个整数参数。那么显然,我们应该能写下表达式 f(3, 4) ,并且这个表达式的值是确定的。 y2 + x 并不算函数,因为 y2 + x(3, 4) 不像是什么经常见到的记法。就算真的要用这种记法的话,我们也不能知道它到底是 13 还是 19。丘奇把 y2 + x 这样的东西叫做 “形式(form)”,形式只有在可以确定其中出现的变量的顺序时才可以转化为函数。这一步骤通过丘奇的 λ 表示法(§7 参考文献 3)完成。
令 ε 为一个形式,其内变量为 x₁, x₂, ⋯, xₙ ,那么 λ((x₁, ⋯, xₙ), ε) 就表示有 n 个参数的函数,返回值为 x₁, ⋯, xₙ 对应替换成各个参数后,形式 ε 的值。比方说, λ((x, y), y2 + x) 是两个参数的函数, λ((x, y), y2 + x)(3, 4) = 19 。
λ 表达式中出现的变量是 “被绑定的”(bound),所以我们可以改变变量的名称,而不会改变表达式的值(当然不能重名)。也就是说 λ((x, y), y2 + x),λ((u, v), v2 + u), λ((y, x), x2 + y) 都是同一个函数。
我们之后会频繁用到这样一种表达式,其中有一些变量出现在 λ 中,而另一些没有。这样的表达式可能被视作带 parameter 6的函数。我们把这些没有绑定的变量称作 “自由变量”。
可以区分形式和函数的记法都可以表示出函数的函数。这里再给例子就容易离题了,不过我们接下来需要用到以函数作为参数的函数。
2.6. 表达式和递归函数
λ 表示法不足以表示递归函数7。比方说,我们可以用 λ 把:
sqrt(a, x, ε) = (|x2 - a| < ε → x, T → sqrt(a, (x + a/x)/2, ε))
转换成:
sqrt = λ((a, x, ε), (|x2 - a| < ε → x, T → sqrt(a, (x + a/x)/2, ε)))
但是等号右侧并不能用作表达式,因为没有办法让 sqrt 表示外层的整个 λ 表达式。
为了编写求值为递归函数的表达式,我们引入一条新的记法。 label(a, ε) 基本上就与表达式 ε 等价,但是其中 a 的出现会被解释为对整个 ε 的引用。因此我们可以编写:
label(sqrt, λ((a, x, ε), (|x2 - a| < ε → x, T → sqrt(a, (x + a/x)/2, ε))))
label(a, ε) 中的符号 a 也是被绑定的,所以替换掉所有的 a 并不会影响表达式的值。不过 label(a, ε) 中 a 的行为和 λ 绑定的变量稍微有些不同就是了。
3. 符号表达式的递归函数
我们首先要定义符号表达式,其中需要用到有序点对和列表。接下来我们定义 5 个基本的函数和谓词,通过组合、条件表达式以及递归构建广阔领域内的函数,并提供大量示例。接下来我们会展示条件表达式以及递归函数如何记作符号表达式,并定义泛应用函数 apply,从而计算从表达式获得的函数在不定数量的参数下的值。最后,我们会定义一些以函数作为参数的函数,并给出一些实用示例。
3.1. 符号表达式
我们现在定义 S-表达式(S 表示 “符号的”,Symbolic)。其由特殊字符:
⋅ ( )
以及一组无穷个符号构成。其中符号是原子,也就是不能继续分成更细的组件。至于符号的表示,我们使用大写拉丁字母、十个数字和单词间空格所构成的字符串。8比方说以下这些都是符号:
- A
- ABA
- APPLE PIE NUMBER 3
不使用类似数学的单个字母有两个原因。第一,计算机程序常常需要数百个可以互相区分的符号,并且需要用 IBM 704 可以显示的 47 个字符表示。第二,用英文单词和短语作为原子比较方便记。因为符号是原子,所以它(作为字符串)的所有子结构都被忽略。我们认为,名字不同的符号是不同的,名字相同的符号是相同的。接下来我们定义 S-表达式:
- 符号是 S-表达式
- 如果 e₁ 和 e₂ 都是 S-表达式,那么 (e₁ ⋅ e₂) 也是。
举个例子,以下这些都是 S-表达式:
- AB
- (A ⋅ B)
- ((AB ⋅ C) ⋅ D)
也就是说,S-表达式是有序的点对结构,各部分均为更简单的 S-表达式或者符号。我们可以用 S-表达式来表示任意长度的列表。给定 n 个元素的列表:
(m₁, m₂, ⋯, mₙ)
我们用这样的 S-表达式来表示它:
(m₁ ⋅ (m₂ ⋅ (⋯ (mₙ ⋅ NIL)⋯)))
其中 NIL 是一个符号,用于表示列表的终止。因为我们要处理的大部分 S-表达式都可以方便地表示为列表,所以我们接下来引入一种特定 S-表达式的缩写:
- (m) 表示 (m ⋅ NIL)
- (m₁, ⋯, mₙ) 表示 (m₁ ⋅ (⋯ (mₙ ⋅ NIL)⋯))
- (m₁, ⋯, mₙ ⋅ x) 表示 (m₁ ⋅ (⋯ (mₙ ⋅ x)⋯))
子表达式可以用类似的方法简化。举两个例子:
- ((AB, C), D) 表示 ((AB ⋅ (C ⋅ NIL)) ⋅ (D ⋅ NIL))
- ((A, B), C, D ⋅ E) 表示 ((A ⋅ (B ⋅ NIL)) ⋅ (C ⋅ (D ⋅ E)))
因为我们把带逗号的表达式视作不带逗号的表达式的缩写,所以我们把它们全都称作 S-表达式。
3.2. S-表达式的函数以及表示它们的表达式
我们接下来定义一类 S-表达式的函数。表示这些函数的表达式是用常规函数符号编写的。但是,为了清楚地区分表示函数的表达式和 S-表达式,我们将使用小写字母序列来表示函数名称和变量,其中变量可以用于 S 表达式中。我们还会在涉及函数时使用方括号和分号,而不是圆括号和逗号。因此以下是合法的函数调用:
- car[x]
- car[cons[(A ⋅ B); x]]
这些 M-表达式(Meta-expression)中所有 S-表达式都表示它们自己。
3.3. 基本 S-函数和 S-谓词
我们引入以下函数和谓词:
-
atom: atom[x] 的值是 T 或者 F ,具体取决于 x 是否是原子。因此
- atom[X] = T
- atom[(X ⋅ A)] = F
-
eq: eq[x; y] 只有在 x 和 y 都是符号时才有定义。如果它们是相同的符号,那么 eq[x; y] = T;否则 eq[x; y] = F 。
-
car: car[x] 只有在 x 不是原子时才有定义。我们定义 car[(e₁ ⋅ e₂)] 为 e₁ ,因此
- car[X] 未定义
- car[(X ⋅ A)] = X
- car[((X ⋅ A) ⋅ Y)] = (X ⋅ A)
-
cdr: cdr[x] 同样在 x 不是原子时才有定义。我们定义 cdr[(e₁ ⋅ e₂)] 为 e₂ ,因此
- cdr[X] 未定义
- cdr[(X ⋅ A)] = A
- cdr[((X ⋅ A) ⋅ Y)] = Y
-
cons: cons[x; y] 对任何 x, y 都有定义。我们定义 cons[e₁; e₂] 为 (e₁ ⋅ e₂) ,因此:
cons[X; A] = (X ⋅ A) cons[(X ⋅ A); Y] = ((X ⋅ A) ⋅ Y)
容易发现 car, cdr 和 cons 之间的关系。
- car[cons[x; y]] = x
- car[cons[x; y]] = y
- car[car[x]; cdr[x]] = x (其中 x 不能是原子)
等之后我们讨论了该系统在计算机中的表示,“car” 和 “cdr” 这两个名称就会有助记符意义了。组合 car 和 cdr 可以获取表达式在指定位置的子表达式。组合 cons 可以用子表达式构造出指定结构的表达式。以这种方式形成的函数非常有限,没有研究价值。
3.4. 递归 S-函数
通过条件表达式和递归函数定义,我们可以得到多得多的函数(实际上,是所有可计算函数)。我们现在给出可以这样定义的几个函数。
-
ff[x] 的返回值是 S-表达式 x 中的第一个原子,忽略括号。比方说
ff[((A ⋅ B) ⋅ C)] = A
我们定义
ff[x] = [atom[x] → x; T → ff[car[x]]]
接下来我们跟踪 ff[((A ⋅ B) ⋅ C)] 求值的每一步:
ff[((A ⋅ B) ⋅ C)] = [atom[((A ⋅ B) ⋅ C)] → ((A ⋅ B) ⋅ C); T → ff[car[((A ⋅ B) ⋅ C)]]] = [F → ((A ⋅ B) ⋅ C); T → ff[car[((A ⋅ B) ⋅ C)]]] = [T → ff[car[((A ⋅ B) ⋅ C)]]] = ff[car[((A ⋅ B) ⋅ C)]] = ff[(A ⋅ B)] = [atom[(A ⋅ B)] → (A ⋅ B); T → ff[car[(A ⋅ B)]]] = [F → (A ⋅ B); T → ff[car[(A ⋅ B)]]] = [T → ff[car[(A ⋅ B)]]] = ff[car[(A ⋅ B)]] = ff[A] = [atom[A] → A; T → ff[car[A]]] = [T → A; T → ff[car[A]]] = A-
subst[x; y; z] 把 S-表达式 z 中出现的所有符号 y 替换为 S-表达式 x。其定义为:
subst[x; y; z] = [atom[z] → [eq[z; y] → x; T → z]; T → cons[subst[x; y; car[z]]; subst[x; y; cdr[z]]]]举个例子,可以求出:
subst[(X ⋅ A); B; ((A ⋅ B) ⋅ C)] = ((A ⋅ (X ⋅ A)) ⋅ C)
-
-
equal[x; y] 是一个谓词,它在两参数为相同 S-表达式时返回 T,其他情况返回 F。我们定义:
equal[x; y] = [atom[x] ∧ atom[y] ∧ eq[x; y]] ∨ [¬atom[x] ∧ ¬atom[y] ∧ equal[car[x]; car[y]] ∧ equal[cdr[x]; cdr[y]]]用 S-表达式的列表缩写法可以方便地看到基本函数长什么样。容易验证:
-
car[(m₁, m₂, ⋯ , mₙ)] = m₁
-
cdr[(ms, m₂, ⋯ , mₙ)] = (m₂, ⋯ , mₙ)
-
cdr[(m)] = NIL
-
cons[m₁; (m₂, ⋯ , mₙ)] = (m₁, m₂, ⋯ , mₙ)
-
cons[m; NIL] = (m)
我们定义
null[x] = atom[x] ∧ eq[x; NIL]
这个谓词在处理列表时很有用。
因为我们经常要组合 car 和 cdr ,所以我们定义如下的缩写:
- cadr[x] 表示 car[cdr[x]]
- caddr[x] 表示 car[cdr[cdr[x]]] ,以此类推
另一个有用的缩写是
list[e₁; e₂; ⋯; eₙ] = cons[e₁; cons[e₂; ⋯ cons[eₙ; NIL]⋯]]
这个函数把所有参数组合成一个列表。
把 S-表达式视作列表时,下面这几个函数会很常用。
-
append[x; y]
append[x; y] = [null[x] → y; T → cons[car[X]; append[cdr[X], y]]]
例如, append[(A, B); (C, D, E)] = (A, B, C, D, E)
-
among[x; y]
该谓词判断 S-表达式是否出现于列表 y 之中,其定义为:
among[x; y] = ¬null[y] ∧ [equal[x; car[y]] ∨ among[x; cdr[y]]]
-
pairs[x; y]
该函数返回二元列表的列表,其中各个元素对应于列表 x 和 y 的元素。
pairs[x; y] = [ null[x] ∧ null[y] → NIL; ¬atom[x] ∧ ¬atom[y] → cons[list[car[x]; car[y]]; pair[cdr[x]; cdr[y]]]]
例如, pair[(A, B, C); (X, (Y, Z), U)] = ((A, X), (B, (Y, Z)), (C, U)) 。
-
assoc[x; y]
如果 y 是列表 ((u₁, v₁), (u₂, v₂), …, (uₙ, vₙ)) ,并且 x 是某一个 u ,那么 assoc[x; y] 是对应的 v 。我们定义:
assoc[x; y] = eq[caar[y]; x] → cadar[y]; T → assoc[x; cdr[y]]例如,
assoc[X; ((W, (A, B)), (X, (C, D)), (Y, (E, F)))] = (C, D) -
sublis[x; y]
其中 x 形如 ((u₁, v₁), ⋯, (uₙ, vₙ)) ,各个 u 都是符号;y 可以是任意 S-表达式。 sublis[x; y] 会把 y 中所有 u 替换为对应的 v 。为了定义这个函数,我们首先定义一个辅助函数:
sub2[x; z] = [ null[x] → z; eq[caar[x]; z] → cadar[x]; T → sub2[cdr[x]; z]]接下来我们定义:
sublis[x; y] = [atom[y] → sub2[x; y]; T → cons[sublis[x; car[y]]; sublis[x; cdr[y]]]]举个例子, sublis[((X, (A, B)), (Y, (B, C))); (A, X ⋅ Y)] = (A, (A, B), B, C)
3.5. 用 S-表达式表示 S-函数
截至目前,S-函数可以用 M-表达式描述。接下来我们给出一种将 M-表达式转换为 S-表达式的规则,以便能够使用 S-函数对 S-函数进行某些计算,进而回答有关 S-函数的某些问题。
转换由以下规则确定,我们用 ε* 表示 M-表达式 ε 转换成 S-表达式的结果。
- 如果 ε 是 S-表达式,那么 ε* = (QUOTE, ε)
- 以小写字母表示的函数名和变量名会被转换成大写。因此 car* = CAR , subst* = SUBST 。
- 式 f[e₁; e₂; ⋯; eₙ] 会转换为 (f*, e₁*, e₂*, ⋯, eₙ*) 。因此 cons[car[x]; cdr[x]]* = (CONS, (CAR X), (CDR X)) 。
- [p₁ → e₁; ⋯ ; pₙ → eₙ]* = (COND, (p₁*, e₁*), ⋯ , (pₙ*, eₙ*))
- λ[[x₁; ⋯ ; xₙ]; E]* = (LAMBDA, (x₁*, ⋯ , xₙ*), E*)
- label[a; E]* = (LABEL, a*, E*)
按照上面这些转换步骤,我们可以把 M-表达式
label[subst; λ[[x; y; z];
[atom[z] → [eq[y; z] → x; T → z];
T → cons[subst[x; y; car[z]];
subst[x; y; cdr[z]]]]]]
转换成 S-表达式:
(LABEL, SUBST,
(LAMBDA, (X, Y, Z),
(COND, ((ATOM, Z), (COND, ((EQ, Y, Z), X), ((QUOTE, T), Z))),
((QUOTE, T), (CONS, (SUBST, X, Y, (CAR, Z)),
(SUBST, X, Y, (CDR, Z)))))))
这种记法是可写的,并且还算稍微有点可读性。如果牺牲结构正规性的话,读写会方便一点。如果电脑上能用的字符更多,那么读写会方便不少。9
3.6. 泛应用函数 apply
令 f’ 是一个 S-函数, f 是其对应的 S-表达式, args 是参数列表,形如 (arg₁, arg₂, ⋯, argₙ) ,其中各个 arg 都是任意 S-表达式。 apply 这个 S-函数满足等式:
apply[f; args] = f’[arg₁; arg₂; ⋯; argₙ]
也就是说,等号左边有定义当且仅当等号右边同样有定义,并且在有定义时它们是相等的。比方说
λ[[x; y]; cons[car[x]; y]][(A, B); (C, D)]
= apply[(LAMBDA, (X, Y), (CONS, (CAR, X), Y));
((A, B), (C, D))]
= (A, C, D)
接下来我们给出 apply 的定义:
apply[f; args] = eval[cons[f; appq[args]]; NIL]
其中
appq[m] = [null[m] → NIL;
T → cons[list[QUOTE; car[m]];
appq[cdr[m]]]]
而更重要的 eval 函数的定义如下:
val[e; a]
= [atom[e] → assoc[e; a];
atom[car[e]]
→ [eq[car[e]; QUOTE] → cadr[e];
eq[car[e]; ATOM] → atom[eval[cadr[e]; a]];
eq[car[e]; EQ] → [eval[cadr[e]; a] = eval[caddr[e]; a]];
eq[car[e]; COND] → evcon[cdr[e]; a];
eq[car[e]; CAR] → car[eval[cadr[e]; a]];
eq[car[e]; CDR] → cdr[eval[cadr[e]; a]];
eq[car[e]; CONS] → cons[eval[cadr[e]; a]; eval[caddr[e]; a]];
T → eval[cons[assoc[car[e]; a];
evlis[cdr[e]; a]];
a]];
eq[caar[e]; LABEL] → eval[cons[caddar[e]; cdr[e]];
cons[list[cadar[e]; car[e]];
a]];
eq[caar[e]; LAMBDA] → eval[caddar[e];
append[pair[cadar[e]; evlis[cdr[e]; a]];
a]]]
其中涉及了两个小函数:
evcon[c; a] = [eval[caar[c]; a] → eval[cadar[c]; a];
T → evcon[cdr[c]; a]]
evlis[m; a] = [null[m] → NIL;
T → cons[eval[car[m]; a];
evlis[cdr[m]; a]]]
接下来我们详细解释这些函数定义的几个要点。10
-
最顶层的 apply 生成一个表达式,表示 “将给定参数应用于给定函数”,并将计算该表达式的工作转移至函数 eval 。它使用 appq 在每个参数周围加上引号,以便 eval 将它们视为常量。
-
eval[e; a] 有两个参数,一个要计算的表达式 e ,以及一个二元列表的列表 a 。每个二元列表的第一项是符号,第二项是该符号所代表的 S-表达式。
-
如果要计算的表达式是一个原子,也就是符号,则 eval 返回列表 a 中最先与它匹配的内容。
-
如果 e 并不是原子,但是 car[e] 是原子,那么表达式必定形如:
- (QUOTE, e)
- (ATOM, e)
- (EQ, e₁, e₂)
- (COND, (p₁, e₁), ⋯, (pₙ, eₙ))
- (CAR, e)
- (CDR, e)
- (CONS, e₁, e₂)
- (f, e₁, …, eₙ), 其中 f 是一个符号
在 (QUOTE, e) 的情况下,直接返回表达式 e 本身。在 (ATOM, e) 或 (CAR, e) 或 (CDR, e) 的情况下,计算表达式 e 并调用适当的函数。如果是 (EQ, e₁, e₂) 或 (CONS, e₁, e₂) ,则需要计算两个表达式。在 (COND, (p₁, e₁), ⋯, (pₙ, eₙ)) 的情况下,按顺序计算 p ,直到找到值为 T 的 p ,然后计算对应的 e 。这是由另一个函数 evcon 完成的。最后,在 (f, e₁, ⋯, eₙ) 的情况下,我们把 f 替换为其在关联表 a 中对应的值,并求值替换后得到的表达式。
-
求值 ((LABEL, f, ε), e₁, ⋯, eₙ) 时,我们将 (f, (LABEL, f, ε)) 放在列表 a 的第一个位置,然后求值 (ε, e₁, ⋯, eₙ) 。
-
最后,求值 ((LAMBDA, (x₁, ⋯, xₙ), ε), e₁, ⋯, eₙ) 时,我们把二元列表的列表11 ((x₁, e₁), ⋯, (xₙ, eₙ)) 拼接到 a 前面,然后求值 ε 。
其实我们也可以不用列表 a ,用参数替换表达式 ε 中变量来求值 LAMBDA 和 LABEL 表达式。可惜,有多个重名的绑定变量时这个操作会非常麻烦,但是只要使用列表 a 就可以绕过这些问题。
使用 apply 计算函数值不适合人类,而适合计算机。但是为了说明它的原理,我们现在给出下面表达式的计算步骤:
apply[(LABEL, FF,
(LAMBDA, (X),
(COND, ((ATOM, X), X),
((QUOTE, T), (FF, (CAR, X))))));
((A ⋅ B))] = A
第一个参数表示我们在 §3.4 节定义的函数 ff 。我们接下来把它简写成 ɸ 。那么我们有:
apply[ɸ; ((A ⋅ B))]
= eval[((LABEL, FF, ψ),
(QUOTE, (A ⋅ B)));
NIL]
(其中 ψ 是 ɸ 中 “ (LAMBDA ⋯) ” 部分)
= eval[((LAMBDA, (X), ω),
(QUOTE, (A ⋅ B)));
((FF, ɸ))]
(其中 ω 是 ψ 中 “ (COND ⋯) ” 部分)
= eval[(COND, (π₁, ε₁), (π₂, ε₂));
((X, (QUOTE, (A ⋅ B))),
(FF, ɸ))]
用 a 表示 ((X, (QUOTE, (A ⋅ B))), (FF, ɸ)) ,我们得到:
= evcon[((π₁, ε₁), (π₂, ε₂)); a]
这会涉及到 eval[π₁; a] ,我们把它展开:
eval[π₁; a]
= eval[(ATOM, X); a]
= atom[eval[X; a]]
= atom[eval[assoc[X; ((X, (QUOTE, (A ⋅ B))), (FF, ɸ))];
a]]
= atom[eval[(QUOTE, (A ⋅ B)); a]]
= atom[(A ⋅ B)]
= F
回到我们的主计算里来,我们现在知道了:
evcon[((π₁, ε₁), (π₂, ε₂)); a]
= evcon[((π₂, ε₂)); a]
这一步又涉及到了 eval[π₂; a] = eval[(QUOTE, T); a] = T 。
= eval[(FF, (CAR, X)); a]
= eval[cons[ɸ; evlis[((CAR, X)); a]; a]]
其中的 evlis[((CAR, X)); a] 求值时会涉及到:
eval[(CAR, X); a]
= car[eval[X; a]]
= car[(A ⋅ B)] (这里我们使用了之前 atom[eval[X; a]] 的计算过程)
= A
因此
evlis[((CAR, X)); a] = list[list[QUOTE, A]] = ((QUOTE, A))
进而,我们的主计算过程可以变为:
eval[cons[ɸ; evlis[((CAR, X)); a]; a]]
= eval[(ɸ, (QUOTE, A)); a]
接下来的计算步骤就跟刚开始时差不多。 LABEL 和 LAMBDA 会向 a 中添加新的二元列表,设结果为 a₁ 。在 cond 表达式中的 π₁ 求值的结果为 eval[π₁; a₁] = eval[(ATOM, X); a₁] = T ,因为在 a₁ 中 X 关联的值为 (QUOTE, A) ,和 a 中不同,在 a 中 X 关联的值是 (QUOTE, (A ⋅ B)) 。
所以 evcon 返回 eval[X; a₁] = A 。
3.7. 以函数作为参数的函数
容易定义出很多以函数作为参数的实用函数。特别是要定义其它函数时,以函数作为参数的函数会更加有用。比方说 maplist[x; f] 这个函数12,其中 x 是一个 S-表达式,而参数 f 是一个单参 S-函数。它的定义是:
maplist[x; f] = [null[x] → NIL; T → cons[f[x]; maplist[cdr[x]; f]]]
接下来,我们编写一个求多元多项式的偏导数的程序,以此说明 maplist 的有用性。我们将要求导的 S-表达式需满足的条件如下。
-
任意符号都是允许的表达式。
-
如果 e₁, e₂, …, eₙ 是允许的表达式,那么
- (PLUS, e₁, e₂, ⋯, eₙ)
- (TIMES, e₁, e₂, ⋯, eₙ)
都是允许的表达式,分别表示和与积。
其实这本质上就是使用前缀表达式的加法和乘法,不同之处在于使用逗号和括号,并且每个运算都可以使用任意个参数。比方说,这个 S-表达式:
(TIMES, X, (PLUS, X, A), Y)
是我们的程序允许的。用常规的代数表示法为:
X(X + A)Y
接下来是偏导公式的定义,其返回多项式 y 对变量 x 的偏导13:
diff[y; x]
= [atom[y] → [eq[y; x] → ONE;
T → ZERO];
eq[car[Y], PLUS]
→ cons[PLUS; maplist[cdr[y]; λ[[z]; diff[car[z]; x]]]];
eq[car[Y], TIMES]
→ cons[PLUS;
maplist[cdr[y];
λ[[z];
cons[TIMES;
maplist[cdr[y];
λ[[w];
[¬eq[z; w] → car[w];
T → diff[car[w]; x]]]]]]]]]
表达式 (TIMES, X, (PLUS, X, A), Y) 对自变量 X 的导数,也就是这个函数的返回值,为
(PLUS, (TIMES, ONE, (PLUS, X, A), Y),
(TIMES, X, (PLUS, ONE, ZERO), Y),
(TIMES, X, (PLUS, X, A), ZERO))
除了上面这个 maplist ,这里再给出一个以函数为参数的实用函数 search :
search[x; p; f; u] = [null[x] → u;
p[x] → f[x];
T → search[cdr[x]; p; f; u]]
这个函数在列表 x 中搜索拥有属性 p 的元素,如果有,那么返回它在 f 下的像;如果这样的元素不存在,那么返回 u。
脚注
1 原文脚注:这篇论文的 LATEX 化有一部分来自 ARPA(ONR) 给斯坦福大学的资助 N00014-94-1-0775,John McCarthy 自 1962 年以来一直在那里工作。该文章从 1960 年 4 月的 CACM(译注:Communication of the Association for Computing Machinery)复制,稍微更改了一些符号。如果您想要准确的排版,请查看那里。现地址,John McCarthy,计算机科学系,斯坦福,CA 94305,(电子邮件:[email protected]),(网址:http://www-formal.stanford.edu/jmc/)
2 译注:实际上并没有 “第二部分”。这篇论文标题里有 “第一部分” 是因为 McCarthy 认为需要 “在另一篇论文中描述 LISP 用于的一些符号计算”。
3 译注:原文为 universal。我将其译为 “泛应用” 是因为这个函数把参数传递给另一个函数,并返回后者返回的值,这一操作通常叫做 “应用”(apply)。而 “泛” 指 apply 接受所有参数组合而成的列表,与之相反的 funcall 就应该叫做 “狭应用”。
4 原文脚注:参考 Kleene
5 原文脚注:我向 CACM 发送了一份关于 Algol 60 中应包含哪些内容的条件表达式提案。由于该项目很短,编辑将其降级为给编辑的一封信,CACM 随后对此道歉。这里给出的符号被 Algol 60 拒绝了,因为它已经决定不使用新的数学符号,新的符号都需要用英语。Algol 60 所采用的 if … then … else 语法由 John Backus 提出。
6 译注:反正这个 parameter 后面也没用到,我就不翻译了。
7 其实是有办法的,也就是 Y 组合子,但是 McCarthy 发表该论文时 Y 组合子还没有被发现。
Y = (λ(f), (λ(x), f(x(x)))((λ(x), f(x(x)))))
或者把 Y 的参数挪到左边:
Y(f) = (λ(x), f(x(x)))((λ(x), f(x(x))))
它有一个重要的性质。令 f 是任意函数,那么:
Y(f) = (λ(x), f(x(x)))((λ(x), f(x(x))))
= f((λ(x), f(x(x)))((λ(x), f(x(x)))))
= f(Y(f))
现代数学语言称 Y(f) 为 f 的 “不动点”,因为其经过 f 映射后不变。接下来我们可以用 Y 组合子来定义递归函数。比方说,阶乘函数可以定义为:
Y(λ((factorial),
(λ((n),
(n = 0 → 1,
T → n ⋅ factorial(n - 1))))))
8 原文脚注:1995 年评论:单词间空格之所以允许,是因为列表的元素之间用逗号分隔。
9 原文脚注:1995: SAIL 上可用的字符更多,不久后 Lisp 机上也有了。哎,世界又跌回劣等字符集了——虽然没有跌到这篇论文完成时,1959 年早期。
10 原文脚注:1995:这个版本并不完全正确。这个和其它版本的 eval,包括真正实现了的(并且调试过的),之间的差距见 Herbert Stoyan 的 “The Influence of the Designer and the Design” 以及 Vladimir Lifschitz (ed.) 于 1991 年的 《Artificial Intelligence and Mathematical Theory of Computation: Papers in Honor of John McCarthy》(标题大意:人工智能与计算的数学理论:John McCarhy 精神引领的论文), Academic Press。
11 译注:此处的 e₁, ⋯, eₙ 应该替换为它们求值后的结果。后面的计算过程中,第三个等号有类似的问题。不过在 eval[π₁; a] 的求值过程中第三个等号又多了一个 eval ,所以最终结果并没有出现问题。
12 译注:现代 LISP 中 maplist 的参数顺序和这里相反。此外,M-表达式并不允许参数出现函数,只能出现变量、S-表达式和其它 M-表达式。不过反正 M-表达式也没有用在计算机上,不严谨也没人在乎。
13 译注:这个函数定义有误。第一个问题在于其 eq[car[Y], TIMES] 子句中 eq,它应该改成 equal,因为 eq 在参数不是原子时返回值是未定义的(见§3.3 节)。第二个问题更难发现,请看这个子句:
eq[car[Y], PLUS] → cons[PLUS; maplist[cdr[y]; λ[[z]; diff[car[z]; x]]]]
其中用到了 x,而 x 实际上并不能表示 diff[y; x] 中的 x,因为这个变量被 maplist 覆盖了。这是词法作用域必要性的一个重要论据,Paul Graham 就在其短文《The Roots of Lisp》中提到了该 bug。此外第 3 子句中也有类似的 bug。
14 译注:Advice Taker 是 McCarthy 在他 1959 年论文《Programs with Common Sense》中提出的概念。该论文描述的假想程序可以看作世界上第一个完整的人工智能系统。
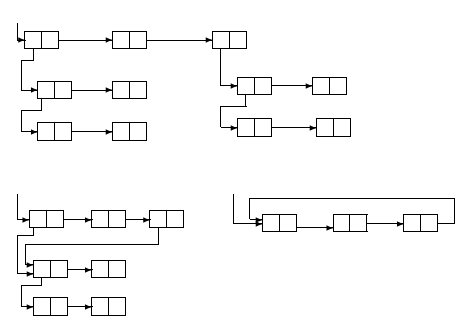
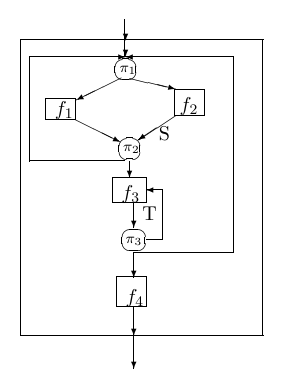
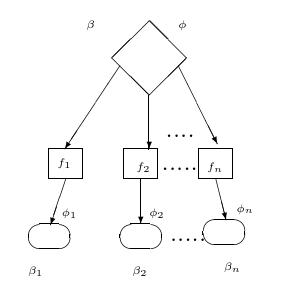
15 译注:图 1 可能在历史长河中丢失了 (a) 和 (b) 标记。我猜上方为 1a,左下方为 1b,右下方为 1c。
16 译注:IBM 704 中有两种指令类型:A 型和 B 型。
- A 型:由 3 比特 “前缀”、15 比特 “减量”、3 比特 “标签” 和 15 比特“地址” 组成。
- B 型:这里用不到。
见 https://bitsavers.org/pdf/ibm/704/24-6661-2_704_Manual_1955.pdf
17 译注:原文为关联表(Association Lists),但是根据原文的脚注 6,后来人们称之为属性表(property list)而不是关联表,所以这里将它译作属性表。
18 原文脚注:我们已经给这个步骤命名为 “垃圾回收”(Garbage Collect)了,但是我不敢在这篇论文里用这个名字——Research Laboratory of Electronics(译注:麻省理工学院的一个实验室)的语法女士们不给我用。
19 译注:“累加器” 指可以存储运算结果的寄存器。现代计算机上所有寄存器都是累加器(甚至内存也是),但是计算机刚出现那会儿累加器很少,比方说 Intel 8080 微处理器就只有一个累加器。
20 译注:然而并没有。我觉着这里的 “例外情况” 指的是间接递归,那样的话用这里的方法(用栈保存临时变量)同样能处理。如果 “例外情况” 指的是尾递归或尾调用的话,那么不需要用栈,直接覆盖可用内存就可以。
21 译注:原文为 “公共后进先出列表”(public push-down list),但是根据原文脚注 8,这种数据结构其实就是栈(stack)。
22 译注:指打孔纸带。它在 1960 年的作用就像磁盘在现代的作用,不用通电也能保留数据的存储器。