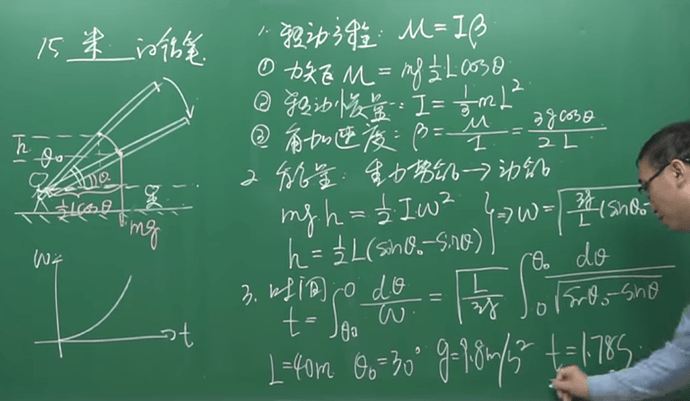Action
2019 年12 月 27 日 17:09
1
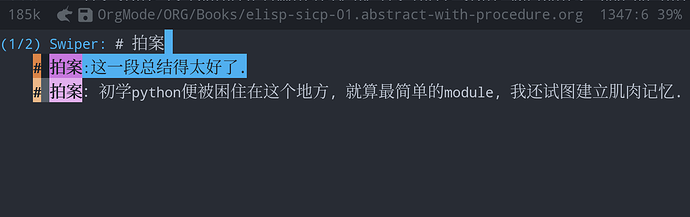
SICP常读常新, 如绘画, 层层递进, 构图, 起形, 框架, 明暗, 光线…
反复阅读, 逐次夯建, 领会书中妙处.
畅想一番, 假如SICP曾经是elisp语言写的(vice versa) 或者在1985年, SICP便有了elisp版本;编辑器圣战或成昨日烟尘, IT行业之外, Emacs或成当今的Office Suites.
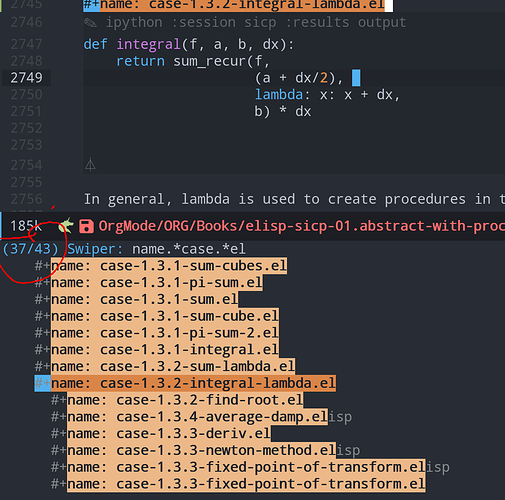
做了点作业, SICP in elisp, 五章五个org文档, 其中前三章全须全尾(原文注脚, 习题, 参考答案等).
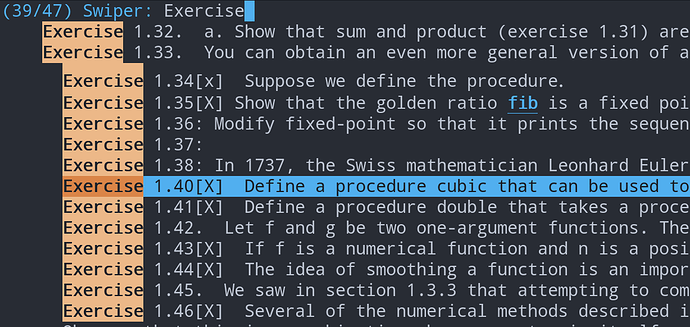
先上第一章: org笔记统计
46道习题
43个课堂案例
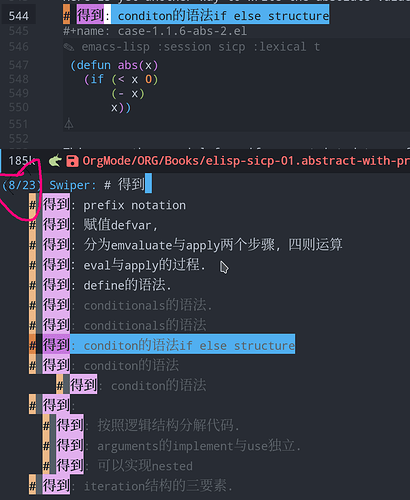
23个语法知识点
个性化笔记:
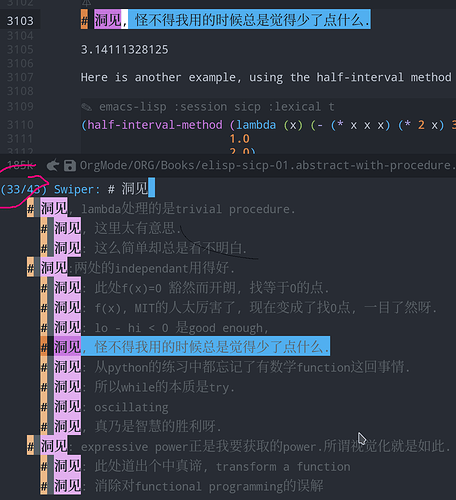
43处启发
两处拍案惊奇
词汇注释
以上笔记仅为打样, 上传到github库的文档, 是一字不多一字不减的书籍正文, 柱脚和图片, 习题参考答案.
10 个赞
Action
2019 年12 月 29 日 00:42
2
李永乐老师最新一期讲了"辅导作业的40米大砍刀"
SICP 1.3.1 黎曼积分公式
(define (integral f a b dx)
(define (add-dx x) (+ x dx))
(* (sum f (+ a (/ dx 2.0)) add-dx b)
dx))
代入
#+name: case-1.3.1-integral.scm
#+BEGIN_SRC scheme :session sicp
(define (f b)
(lambda (x) (/ 1 (sqrt
(- (sin x)
(sin b))))))
(define pi 3.141592653589793)
(define (integral2 f a b dx)
(define (add-dx x) (+ x dx))
(* (sum (f b)
(+ a (/ dx 2.0))
(lambda (x) (+ x dx))
b)
dx))
(* (integral2 f 0 (/ pi 6) 0.00001)
(sqrt (/ 40
(* 3 9.8))))
#+END_SRC
#+RESULTS: case-1.3.1-integral.scm
: 0.0-1.777598336021436i
1.777 vs 1.78
Action
2019 年12 月 29 日 10:14
4
第一章中有趣的语法练习题
Exercise 1.5
Ben Bitdiddle has invented a test to determine whether the interpreter he is faced with is using applicative-order evaluation or normal-order evaluation. He defines the following two procedures:
#+BEGIN_SRC elisp
(defun p (p)) ;; def foo(): return foo()
(defun test(x y)
(if (= x 0)
0
y))
#+END_SRC
Exercise 1.6.
Alyssa P. Hacker doesn’t see why if needs to be provided as a special form. ``Why can’t I just define it as an ordinary procedure in terms of cond?‘’ she asks. Alyssa’s friend Eva Lu Ator claims this can indeed be done, and she defines a new version of if:
#+name: case-1.1.7-ternamy.el
#+begin_src emacs-lisp :session sicp :lexical t :results none
;; ternamy conditions
(defun new-if (predicate then-clause else-clause)
(cond (predicate then-clause)
(t else-clause)))
#+end_src
Delighted, Alyssa uses new-if to rewrite the square-root program:
What happens when Alyssa attempts to use this to compute square roots? Explain.
#+begin_src emacs-lisp :session sicp :lexical t
(defun sqrt-iter(guess x)
(new-if (good-enough-p guess x)
guess
(sqrt-iter (improve guess x)
x)))
(sqrt-iter 1 10)
#+end_src
Exercise 1.34
Suppose we define the procedure.
#+BEGIN_SRC scheme
(define (f g)
(g 2))
(f square)
#+END_SRC
#+RESULTS:
: (f (lambda (z) (* z (+ z 1))))
6
What happens if we (~perversely~) ask the interpreter to evaluate the combination (f f)? Explain.
SICP中的习题与正文遥相呼应, 习题既是前文的总结又是后文的引子.
比如sqrt一共给出了11种解法.
Action
2019 年12 月 30 日 23:52
6
02. Abstraction with data
2.3.1 思路清晰的微分求导公式
#+name: case-2.3.1-symbolic-differentiationl.el
#+begin_src emacs-lisp :session sicp :lexical t
(defun deriv(exp var) ;;v
(cond ((numberp exp) 0) ;
((variable-p exp)
(if (same-variable-p exp var) 1 0)) ;;else 0
((sum-p exp)
(make-sum (deriv (addend exp) var) ;;
(deriv (augend exp) var)))
((product-p exp)
(make-sum
(make-product (multiplier exp)
(deriv (multiplicand exp) var))
(make-product (deriv (multiplier exp) var)
(multiplicand exp))))
(t
(error "unknown expression type -- DERIV" exp))))
;; variable
(defun variable-p(x) (symbolp x))
(defun same-variable-p(v1 v2)
(and (variable-p v1) (variable-p v2) (equal v1 v2)))
;; constructor for sum and product
(defun make-sum(a1 a2) (list '+ a1 a2))
(defun make-product(m1 m2) (list '* m1 m2))
;; predicate and selectors for sum
(defun sum-p(x)
(and (consp x) (equal (car x) '+)))
(defun addend(s) (cadr s))
(defun augend(s) (caddr s))(cadddr '(+ 1 2 3 4))
;; predicate and seletors for product
(defun product-p(x)
(and (consp x) (equal (car x) '*)))
(defun multiplier(p) (cadr p))
(defun multiplicand(p) (caddr p))
#+end_src
#+RESULTS: summary
: multiplicand
#+begin_src emacs-lisp :tangle yes :results output
(print (deriv '(+ x 3) 'x))
(print (deriv '(* x y) 'x))
(print (deriv '(* (* x y) (+ x 3)) 'x))
#+end_src
#+RESULTS:
:
: (+ 1 0)
:
: (+ (* x 0) (* 1 y))
:
: (+ (* (* x y) (+ 1 0)) (* (+ (* x 0)
Action
2019 年12 月 31 日 00:23
7
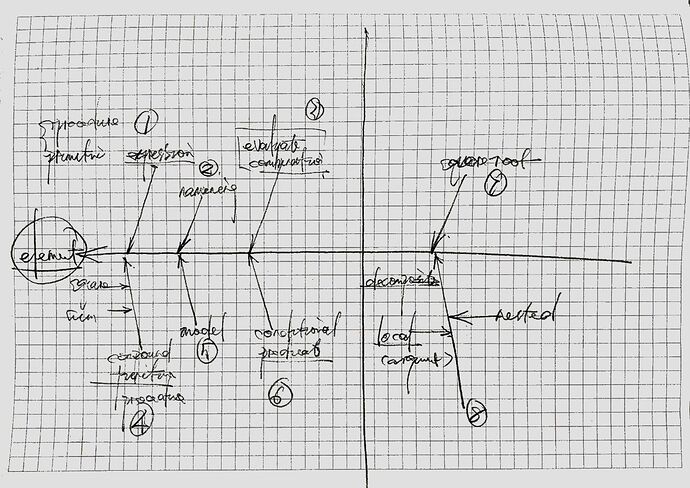
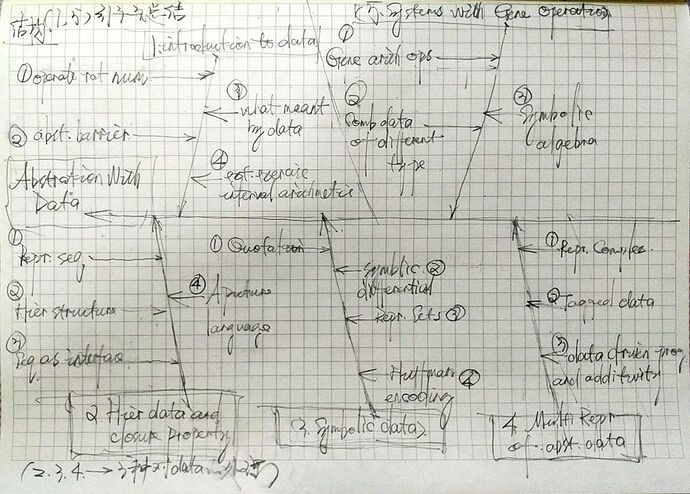
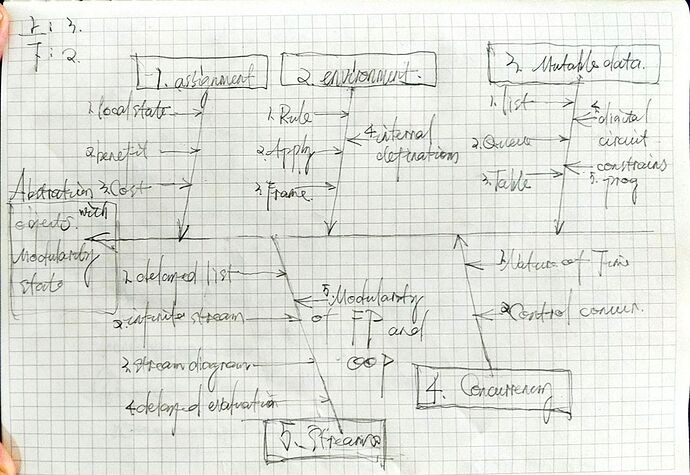
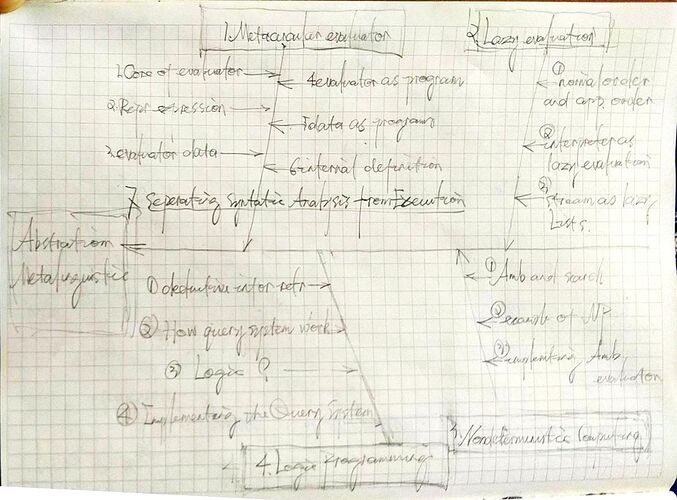
鱼骨图-质量管理七工具之一。
1 个赞
既然读SICP, 不可避免要运行scheme,
如果只拿一个充分的理由:https://docs.racket-lang.org/racket-cheat/index.html#(section._.Essentials)
文档
https://docs.racket-lang.org/guide/index.html
另外还有sicp专题等.
设置很简单,
首先从babel中将scheme打开
(org-babel-do-load-languages 'org-babel-load-languages '(
(scheme . t)
))
然后安装racket
sudo apt install racket
最后从配置中添加一行
(add-hook 'scheme-mode-hook 'geiser-mode)
(setq geiser-default-implementation 'racket)
OK了.
#+begin_src scheme :session sicp
(* 3 3)
#+end_src
#+RESULTS:
: 9
3.Modularity, Objects and State
1 个赞
4.Metalinguistic Abstration
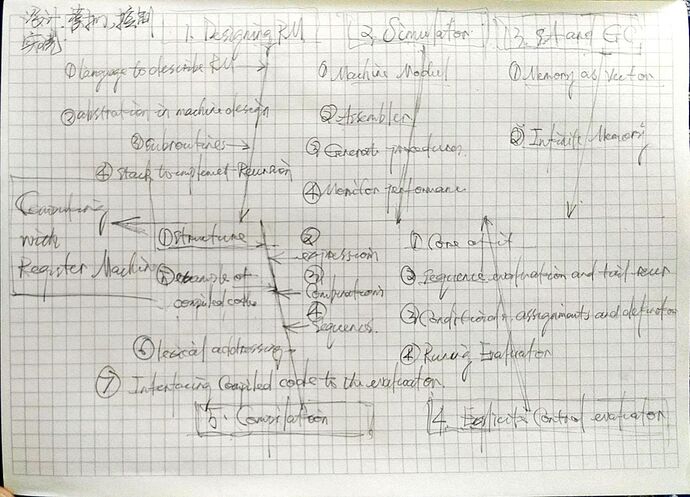
5.Computing with Register Machines
1 个赞
练习
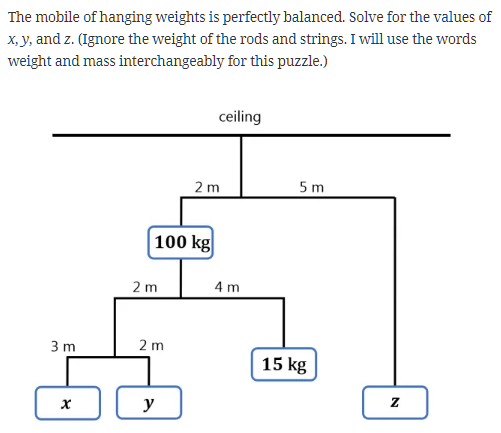
Exercise 2.29. A binary mobile consists of two branches, a left branch and a right branch. Each branch is a rod of a certain length, from which hangs either a weight or another binary mobile. We can represent a binary mobile using compound data by constructing it from two branches (for example, using list):
中的 A binary mobile 是这样的toy
(家里的风铃
1 个赞
sadhen
2024 年8 月 20 日 17:52
15
学SICP用 Emacs Lisp有一点缘木求鱼了
用墨干学SICP目前应该是最好的选择
sadhen
2024 年8 月 21 日 02:44
16
https://gitee.com/LiiiLabs/goldfish
GitHub - LiiiLabs/goldfish: Goldfish Scheme / 金鱼Scheme
这是我发起的一门 Scheme 语言实现,目前是基于 S7 Scheme。
金鱼Scheme 是一个 Scheme 解释器,具有以下特性:
兼容 R7RS-small 标准
提供类似 Python 的标准库
小巧且快速
金鱼Scheme基于S7 Scheme实现,本身不做Scheme解释器,而是在做Scheme标准库。
比如
(import (liii string))
可以替代
(import (srfi srfi-13))
又如:
(import (liii os))
(mkdir "/tmp/hello")
如果你不用 liii 开头的库,scheme开头的R7RS定义的标准库,和srfi开头的SRFI里面定义的函数库,是非常稳定的。
目前还在快速迭代演进的阶段,如果用于生产,不建议使用 liii 开头的标准库。
我自己发起了一个Scheme语言的实现,而且我正在写一本Scheme的书《零基础Scheme》。感兴趣跟着视频一起学吧。